
출처: https://datasets.activeloop.ai/docs/ml/datasets/mnist/
딥러닝을 활용하여 손글씨 숫자 이미지(MNIST 데이터셋)를 분류하는 모델을 구축한다. MNIST는 0부터 9까지의 손글씨 숫자 이미지(28x28 픽셀)로 구성된 대표적인 이미지 분류 데이터셋이다. 이 문제는 10개의 클래스를 분류하는 다중 클래스 분류 문제이다.

TensorFlow의 keras.datasets 모듈을 통해 MNIST 데이터를 로딩한다. 학습 데이터 60,000개와 테스트 데이터 10,000개로 구성되어 있으며, 각 데이터는 28x28 크기의 흑백 이미지이다. 이미지를 시각화하여 각 숫자의 라벨이 잘 매칭되는지 확인한다.




이미지 데이터를 정규화하기 위해 0 ~ 255의 픽셀 값을 0 ~ 1 사이로 스케일링한다. 또한 모델 입력 형식에 맞게 데이터를 reshape 하며, 라벨은 원-핫 인코딩 처리한다. CNN 모델에서는 이미지 차원을 (28, 28, 1)로 변경한다.

딥러닝 모델로는 두 가지 방식을 사용한다.

테스트 데이터 중 하나를 선택하여 예측을 수행하고, 예측 결과를 이미지와 함께 시각화한다. 또한, 테스트 데이터 일부를 이용해 전체 정확도를 평가한다.
학습된 CNN 모델의 정확도는 테스트 데이터에서 약 98% 이상임을 확인한다. Confusion Matrix와 Classification Report를 통해 클래스 별 정밀도와 재현율도 분석한다. 이로써 모델이 손글씨 숫자를 잘 분류함을 확인한다.
• Precision
정확도. 특정 클래스(양성 등)로 예측된 값 중 실제로 해당 클래스인 비율. \[ \text{Precision} = \frac{TP}{TP + FP} \]
• Recall
재현율. 실제 해당 클래스 중 모델이 정확히 예측한 비율.
\[ \text{Recall} = \frac{TP}{TP + FN} \]
• F1-Score
Precision과 Recall의 조화 평균.
\[ \text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} \]
• Support
각 클래스의 실제 데이터 개수.
Classification Report:
precision recall f1-score support
0 0.98 1.00 0.99 42
1 1.00 1.00 1.00 67
2 0.98 0.98 0.98 55
3 0.98 1.00 0.99 45
4 1.00 1.00 1.00 55
5 1.00 0.98 0.99 50
6 1.00 0.98 0.99 43
7 0.98 1.00 0.99 49
8 1.00 0.97 0.99 40
9 1.00 1.00 1.00 54
accuracy 0.99 500
macro avg 0.99 0.99 0.99 500
weighted avg 0.99 0.99 0.99 500
행은 실제 클래스, 열은 예측 클래스이다.
| Actual (실제) | Predicted (예측) | |
|---|---|---|
| Positive (긍정) | Negative (부정) | |
| Positive (긍정) | TP | FN |
| Negative (부정) | FP | TN |
• True Positive (TP)
실제로 긍정이고 모델도 긍정으로 예측한 경우
• True Negative (TN)
실제로 부정이고 모델도 부정으로 예측한 경우
• False Positive (FP)
실제로 부정인데 모델이 긍정으로 잘못 예측한 경우 (Type I Error)
• False Negative (FN)
실제로 긍정인데 모델이 부정으로 잘못 예측한 경우 (Type II Error)
Confusion Matrix:
[[42 0 0 0 0 0 0 0 0 0]
[ 0 67 0 0 0 0 0 0 0 0]
[ 0 0 54 0 0 0 0 1 0 0]
[ 0 0 0 45 0 0 0 0 0 0]
[ 0 0 0 0 55 0 0 0 0 0]
[ 0 0 0 1 0 49 0 0 0 0]
[ 1 0 0 0 0 0 42 0 0 0]
[ 0 0 0 0 0 0 0 49 0 0]
[ 0 0 1 0 0 0 0 0 39 0]
[ 0 0 0 0 0 0 0 0 0 54]]
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
딥러닝 모델은 다양한 라이브러리를 사용한다.
이를 위해 가장 먼저 사용할 라이브러리를 추가한다.
from tensorflow.keras.models import Sequential
keras의 models 중 Sequential 함수를 사용한다.
from은 어디에서 가지고 오는지를 의미하고,
import는 특정 함수를 가져오는 것을 의미한다.
from tensorflow.keras.layers import Dense, Activation
keras의 layers 중 Dense와 Activation 함수를 사용한다.
from tensorflow.keras.utils import to_categorical
keras의 utils 중 to_categorical 함수를 사용한다.
from tensorflow.keras.datasets import mnist
keras의 datasets 중 mnist 데이터셋을 불러온다.
import numpy as np
as 명령어로 함수 이름을 np로 줄여서 사용할 수 있다.
import matplotlib.pyplot as plt
pyplot 라이브러리를 사용하며,plt라고 줄여서 쓴다.
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print("X_train shape", x_train.shape)
print("y_train shape", y_train.shape)
print("X_test shape", x_test.shape)
print("y_test shape", y_test.shape)
▶ 실행 결과
x_train shape (60000, 28, 28)
y_train shape (60000,)
x_test shape (10000, 28, 28)
y_test shape (10000,)
인공지능 모델을 만들려면 훈련(train) 데이터와 검증(test) 데이터가 필요하다. 이것은 마치 우리가 학교에서 보는 시험과 같다. 시험 공부할 때는 시험에 무엇이 나올지 알 수 없다. 그래서 여러 내용을 공부한 후 이를 바탕으로 시험을 본다. 인공지능도 마찬가지이다. 인공지능 성능을 살펴보기 위해 학습에 사용한 데이터로 성능을 평가하는 것은 의미가 없다. 학습에 사용하지 않은 데이터를 얼마나 잘 알아 맞히는지가 그 인공지능 성능을 결정한다.
(x_train, y_train), (x_test, y_test) = mnist.load_data()
mnist 데이터셋 중에 포함된 load_data()라는 함수로 MNIST 데이터셋에서 데이터를 불러온다.
MNIST 데이터셋은 이미 네 부분으로 나뉘어 있는데
첫 번째 부분을 x_train으로,
두 번째 부분을 y_train으로,
세 번째 부분을 x_test로,
마지막 부분을 y_test로 불러온다.
reshape 함수 같은 여러 함수를 사용할 수 있다.
print("X_train shape", x_train.shape)
print를 사용하여 x_train 데이터의 형태를 출력한다.
print 함수 안에 있는 따옴표 문자(x_train shape)는
문자 그대로 출력되지만, 따옴표 안에 있지 않은 문자는 그 값으로 출력된다.
이 명령어를 실행하면 x_train.shape가 가진 값이 출력된다.
x_train.shape는 어떤 값을 가지고 있을까?
shape는 넘파이 라이브러리에서 사용하는 명령어로 데이터의 형태를 볼 수 있다.
이 코드를 실행한 결괏값은 x_train shape (60000, 28, 28)이다.
x_train 데이터에는 총 60,000개의 데이터가 있으며,
각 데이터에는 가로 28개,세로 28개의 데이터가 있다. 즉, x_train
데이터의 모습은 3차원(60000 x 28 x 28)이다.
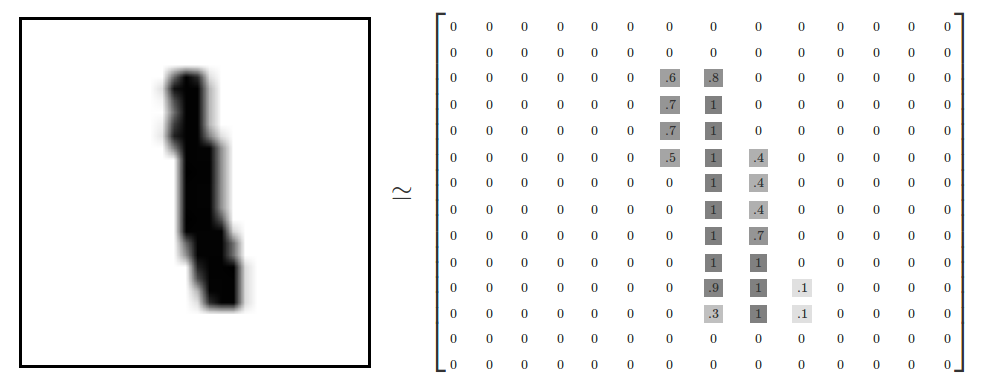
이 중에서 첫 번째 데이터의 실제 모습은 다음 그림과 같다.
숫자 6을 나타내는 그림이다.
검은색은 0, 흰색은 255, 회색은 1 ~ 254 사이의 숫자로(또는 검은색은 0, 흰색은 1, 회색은 0 ~ 1 사이의 숫자로) 나타낸다.
가로 28개의 숫자와 세로 28개의 숫자로 구성된 것을 볼 수 있다.

print("y_train shape", y_train.shape)
print를 사용하여 y_train 데이터의 형태를 출력한다.
y_train 데이터는 x_train 데이터의 정답이다.
x_train의 데이터 개수가 60,000개였으니,
y_train 데이터 또한 60,000개이다.
y_train shape (60000,)이다.
데이터 개수가 60,000개이며,그 뒷부분에는 아무런 정보가 없다.
이렇게 콤마(,) 이후에 아무것도 나오지 않으면 이것은 1차원 배열을 의미한다.
print("X_test shape", x_test.shape)
print를 사용하여 x_test 데이터의 형태를 출력한다.
결괏값은 x_test shape(10000, 28, 28)이다.
참고로 x_train 데이터는 60,000개였지만,
x_test 데이터는 10,000개이다.
print("y_test shape", y_test.shape)
print를 사용하여 y_test 데이터의 형태를 출력한다.
결괏값은 y_test shape(10000,)이다.
참고로 y_train 데이터는 60,000개였지만,
y_test 데이터는 10,000개이다.
X_train = x_train.reshape(60000, 784)
X_test = x_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print("X Training matrix shape", X_train.shape)
print("X Testing matrix shape", X_test.shape)
▶ 실행 결과
X Training matrix shape (60000, 784)
X Testing matrix shape (10000, 784)
28×28 형태의 데이터를 인공지능 모델에 넣으려면 형태를 바꿔야 한다.
인공신경망의 입력층에 데이터를 넣을 때는 한 줄로 만들어서 넣어야 한다.

X_train = x_train.reshape(60000, 784)
x_train 데이터를 1×784로 바꾼다.
이때 사용하는 reshape는 넘파이의 함수이고,
이 함수를 사용하여 데이터 형태를 원하는 대로 바꿀 수 있다.
784는 28×28을 한 값이다.
그렇기 때문에 reshape(60000, 784)은 (60000, 28, 28)를 (60000, 784)로 데이터 형태를 바꾼다.
X_test = x_test.reshape(10000, 784)
x_test 데이터를 1×784로 바꾼다.
즉, (10000, 28, 28)에서 (10000, 784)로 데이터 형태가 바뀐다.
X_train = X_train.astype('float32')
X_train 데이터는 정수형이므로 실수형으로 자료형태를 바꾸어야 한다.
이를 위해 astype 함수를 사용하여 X_train 데이터 형태를 실수 형태(float32)로 바꾸고
그 데이터를 X_train 변수에 다시 넣는다.
X_test = X_test.astype('float32')
X_test 데이터 또한 정규화를 하기 위해 실수형 자료로 바꾸어 준다.
그리고 바꾼 데이터를 X_test 변수에 다시 넣는다.
X_train /= 255
X_train의 각 데이터를 255로 나눈 값을 X_train에 다시
저장한다.
X_test /= 255
X_test의 각 데이터를 255로 나눈 값을 X_test에 다시 저장한다.
print("X Training matrix shape", X_train.shape)
X_train 데이터의 바뀐 형태를 출력한다. 출력 결괏값은 (60000, 784)이다.
print("X Testing matrix shape", X_test.shape)
X_test 데이터의 바뀐 형태를 출력한다. 출력 결괏값은 (10000, 784)이다.
nb_classes = 10
Y_train = to_categorical(y_train, nb_classes)
Y_test = to_categorical(y_test, nb_classes)
print("Y Training matrix shape", Y_train.shape)
print("Y Testing matrix shape", Y_test.shape)
▶ 실행 결과
Y Training matrix shape (60000,10)
Y Testing matrix shape (10000,10)
y_train 데이터와 y_test 데이터의 형태를 바꾸어 보자.
인공지능이 분류를 잘할 수 있도록 하기 위해서이다.
우리가 만들고 있는 인공지능은 이미지를 0~9 사이의 숫자로 분류하는 인공지능이다.
이를 다시 살펴보면 인공지능은 이미지가 가진 숫자의 특성,즉 “이 숫자는 3이고
2보다 1이 더 큰 수다.”와 같은 특성은 알 필요 없다.
우리가 만드는 인공지능의 목표는 3과 2를 잘 구분하기만 하면 된다.
따라서 이미지의 레이블(label, 정답)을 인공지능에 0, 1, 2, 3, 4, ···처럼 숫자로 알려 주는 것이 아니라 더 잘 구분할 수 있는 방법으로 알려 줄 필요가 있다. 바로 0은 0이라는 숫자 의미보다 인공지능이 구분할 10개의 숫자 중 첫 번째 숫자로, 1은 1이라는 숫자 의미보다 두 번째 숫자로 말해 주는 것이다.
이를 조금 어려운 말로 표현하면 수치형 데이터를 범주형 데이터로 변환하는 것이라고 할 수 있다. 이와 같이 몇 번째라는 식으로 알려 주면 인공지능은 더 높은 성능으로 분류할 수 있다. 그래서 예측이 아닌 분류 문제에서는 대부분 정답 레이블을 첫 번째,두 번째,세 번째처럼 순서로 나타내도록 데이터 형태를 바꾼다. 이때 사용하는 방법이 바로 원-핫 인코딩(one-hot incoding)이다.
nb_classes = 10
nb_classes는 "number of classes"이며,
분류 문제에서 클래스의 개수를 나타낸다. 즉, 10개의 클래스로 분류하는 문제이다.
to_categorical 함수를 사용하기 위해서 변경 전 데이터(y_train)와
원-핫 인코딩할 숫자,즉 몇 개로 구분하고자 하는지가 필요하다.
인공지능이 예측하는 결과는 0~9의 숫자이므로 분류하고자 하는 값은 10개이다. 따라서
원-핫 인코딩을 위해 구분하려는 수를 10으로 설정하였다.
Y_train = to_categorical(y_train, nb_classes)
Y_train 데이터를 원-핫 인코딩한다.
이때 사용하는 함수가 텐서플로의 케라스 내부 유틸(utils) 도구인 to_categorical이다.
to_categorical 함수는 수치형 데이터를 범주형 데이터로 만들어 준다.
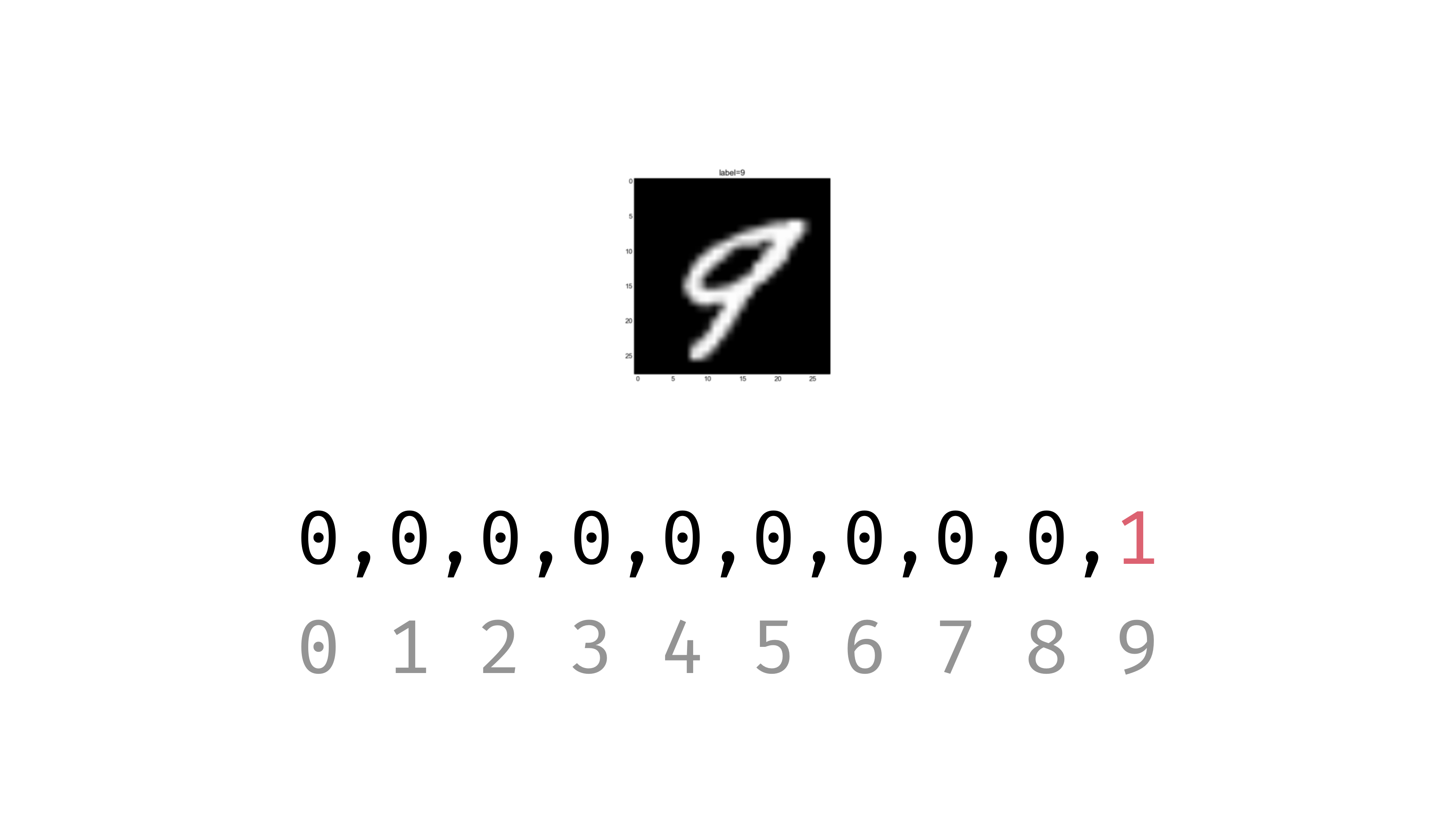
Y_train 데이터가 다음 그림과 같은 형태로 바뀌었다.
9는 10번째에만 1로 표시된 [0, 0. 0, 0, 0, 0, 0, 0, 0, 1]로 바뀌었다.
Y_test = to_categorical(y_test, nb_classes)
y_test 데이터를 원-핫 인코딩하여 Y_test에 넣는다.
print("Y Training matrix shape", Y_train.shape)
Y_train 데이터의 바뀐 형태를 출력해 보자.
출력 결괏값은 (60000, )에서 (60000, 10)로 변형되었다.
즉, 각 행의 데이터 개수가 1개(수치형 데이터)에서 10개(범주형 데이터)로 늘어났기 때문이다.
print("Y Testing matrix shape", Y_test.shape)
Y_test 데이터의 바뀐 형태를 출력해 보자.
이 또한 출력 결괏값은 (10000, )에서 (10000, 10)로 변형되었다.
이와 같이 인공지능을 만들기 위해서는 데이터를 인공지능 모델에서 요구하는 방향으로 분석하여 변환하는 것이 중요하다.
model = Sequential()
model.add(Dense(512, input_shape=(784,)))
model.add(Activation('relu'))
model.add(Dense(256))
model.add(Activation('relu'))
model.add(Dense(10))
model.add(Activation('softmax'))
model.summary()
▶ 실행 결과
Model: "sequential"
------------------------------------
Layer (type) Output Shape Param #
====================================
dense(Dense) (None, 512) 401920
------------------------------------
activation (Activation) (None, 512) 0
------------------------------------
dense_1 (Dense) (None, 256) 131328
------------------------------------
activation_1 (Activation) (None, 256) 0
------------------------------------
dense_2(Dense) (None, 10) 2570
------------------------------------
activation_2 (None, 10) 0
====================================
Total params: 535,818
Trainable params: 535,818
Non-trainable params: 0
우리가 설계하고 있는 인공지능 모델은 4개의 층으로 되어 있다. 첫 번째 층은 입력층으로 데이터를 넣는 층이다. 두 번째와 세 번째 층은 은닉층이다. 마지막 네 번째 층은 결과가 출력되는 출력층이다.
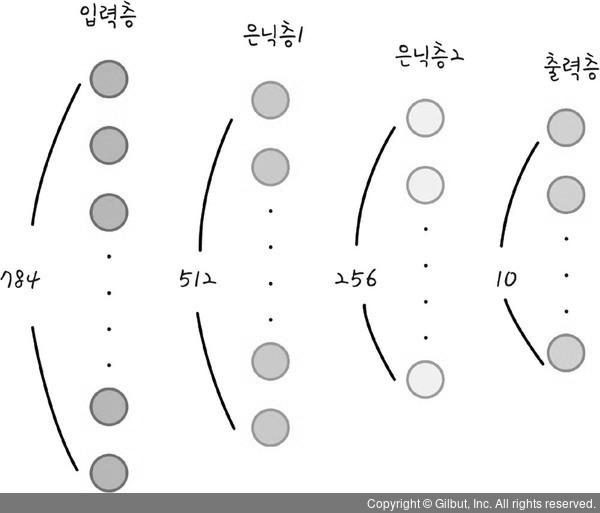
우리가 넣는 784개의 데이터가 한 줄로 되어 있기 때문에 입력층의 뉴런 수는 784이다. 앞에서 우리는 28X28 픽셀로 숫자 모습을 784개의 한 줄로 바꾸었다. 이제 이 데이터를 딥러닝 모델에 넣을 예정이며, 첫 번째 은닉층의 노드는 512개로 설정해 보았다. 첫 번째 은닉층에서 두 번째 은닉 층으로 갈 때 활성화(Activation) 함수는 렐루(ReLU) 함수를 사용할 예정이다.
두 번째 은닉층의 노드는 256개로 설정하였다. 여기서 마지막 층으로 갈 때도 활성화 함수는 렐루 함수를 사용할 예정이다. 마지막 노드가 10개인 이유는 입력된 이미지를 10개로 구분하기 위함이다. 그리고 가장 높은 확률값으로 분류하기 위해서 각 노드의 최종값을 소프트맥스(softmax) 함수를 사용하여 나타내었다.
model = Sequential()
summary 출력결과
Model: “sequential”
model.add(Dense(512, input_shape=(784,)))
add 함수를 사용하여 층을 추가한다.
바로 앞에서 만든 딥러닝 모델(model)이 가지고 있는 함수를 사용하기 때문에
model 뒤에 점을 찍은 후 add 함수를 적는다.
Dense 함수를 사용한다.
Dense 함수의 첫 번째 인자는 해당 은닉층 의 노드 수이며,
두 번째 인자인 input_shape는입력하는 데이터 형태이다.
우리가 입력하는 데이터 형태(input_shape)는 (784, )이며,
첫 번째 은닉층의 노드는 512개로 구성하였다.
summary 출력결과
dense(Dense) (None, 512) 401920
model.add(Activation('relu'))
model.add(Dense(256))
summary 출력결과
dense_1 (Dense) (None, 256) 131328
model.add(Activation('relu'))
model.add(Dense(10))
summary 출력결과
dense_2(Dense) (None, 10) 2570
model.add(Activation('softmax'))
softmax를 사용한다.
model.summary()
summary는 모델이 어떻게 구성되었는지 살펴보는 함수이다.
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, Y_train, batch_size=128, epochs=10, verbose=1)
▶ 실행 결과
Epoch 1/10
469/469 - 9ms/step - loss: 0.2277 - accuracy: 0.9339
Epoch 2/10
469/469 - 9ms/step 一 loss: 0.0816 - accuracy: 0.9747
Epoch 3/10
469/469 - 9ms/step - loss: 0.0522 - accuracy: 0.9840
Epoch 4/10
469/469 - 9ms/step - loss: 0.0348 - accuracy: 0.9890
Epoch 5/10
469/469 - 9ms/step - loss: 0.0267 - accuracy: 0.9915
Epoch 6/10
469/469 - 9ms/step - loss: 0.0222 - accuracy: 0.9926
Epoch 7/10
469/469 - 9ms/step - loss: 0.0179 - accuracy: 0.9940
Epoch 8/10
469/469 - 9ms/step - loss: 0.0173 - accuracy: 0.9941
Epoch 9/10
469/469 - 9ms/step - loss: 0.0144 - accuracy: 0.9952
Epoch 10/10
469/469 - 9ms/step - loss: 0.0112 - accuracy: 0.9963
모델을 설계한 후 이 모델을 실행하기 전에 필요한 것이 있다. 심층신경망에 데이터를 흘려보낸 후 정답을 예측할 수 있도록 신경망을 학습하는 과정이 필요하다. 즉, 딥러닝(Deep Learning, DL)을 해야 한다.
데이터를 사용하여 심층 신경망을 딥러닝 기법으로 학습시킨다. 이때 신경망이 예측한 결과와 실제 정답을 비교한 후 오차가 있다면 다시 신경망을 학습시키는 과정을 거친다. 오차가 없다면 더 학습시킬 필요는 없지만 웬만해서는 오차가 0으로 나오는 경우는 거의 없다. 보통 학습시 키는 횟수를 정한 후 그만큼만 학습시킨다.
이처럼 신경망을 잘 학습시키려면 학습한 신경망이 분류한 값과 실젯값의 오차부터 계산해야 한다. 오차를 줄이는 데 경사 하강법(Gradient Descent Method)을 사용한다.
실행 결과를 보면, 첫 번째 에포크(epoch)부터 열 번째 에포크로 갈수록 오차값(loss)이 줄어드는 것을 볼 수 있다. 정확도(accuracy) 또한 지속적으로 증가하는 것을 볼 수 있다.
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
compile 함수를 제공한다.
이 함수를 사용하는 데 몇 가지 규칙이 있다.
categorical.crossentropy 방법을 사용한다.
optimizer)를 사용한다.
옵티마이저에는 다양한 방법이 있지만 여기에서는 adam이라는 방법을 사용한다.
[Note] 옵티마이저(optimizer)
딥러닝으로 인공지능 모델을 학습시킬 때 발생하는 오차를 줄이려고 경사 하강법이라는 알고리즘을 사용한다.
이때 경사 하강법을 어떤 방식으로 사용할지 다양한 알고리즘이 있는데
그러한 알고리즘을 케라스에서 모아 놓은 것이 바로 옵티마이저 라이브러리다.
옵티마이저 종류에는 아담(adam), 확률적 경사 하강법(SGD) 등이 있다.
model.fit(X_train, Y_train, batch_size=128, epochs=10, verbose=1)
fit 함수를 제공한다. 이 함수를 사용하려면 다음 규칙을 따라야 한다.
X_train, Y_train 데이터를 사용하여 인공지능 모델을 학습하기 때문에 이 두 가지를 입력 데이터로 넣는다.
batch_size)를 정한다. 배치 사이즈란 인공지능 모델이 한 번에 학습하는 데이터 개수를 의미한다. 여기에서는 한 번에 128개의 데이터를 학습시킨다. 즉,배치 사이즈는 128로 한다.
verbose는 1로 설정했다. verbose는 케라스 fit 함수의 결괏값을 출력하는 방법을 의미한다. verbose 값은 0, 1,2 중 하나로 결정할 수 있다.
score = model.evaluate(X_test, Y_test)
print('Test score:', score[0])
print('Test accuracy:', score[1])
▶ 실행 결과
313/313 2ms/step - loss: 0.0817 - accuracy: 0.9800
Test score: 0.08166316896677017
Test accuracy: 0.9800000190734863
지금까지 심층 신경망 모델을 설계하고,그 모델을 학습시켰다. 이제 인공지능 모델 성능이 어느 정도인지 시험해 보자. 시험 내용은 ‘검증 데이터를 얼마나 잘 맞히는가?’이다.
score = model.evaluate(X_test, Y_test)
evaluate 함수는 모델 정확도를 평가할 수 있는 기능을 제공한다. 이 함수를 사용하려면 다음 두 가지 데이터를 넣어야 한다.
X_test를 입력한다.
Y_test를 입력한다.
evaluate 함수에 이 데이터를 넣으면 두 가지 결과를 보여 준다.
X_test,Y_test 데이터를 입력하여 얻은 두 가지 결괏값인 오차와 정확도를 score 변수에 넣는다.
print('Test score:', score[0])
score 변수에는 오차값과 정확도가 들어 있다. 여기에서는 오차값을 출력하기 위해 score 변수의 첫 번째 항목인 점수를 출력한다. score[0]에서 숫자가 1이 아니고 0인 이유는 첫 번째가 0으로 시작하기 때문이다.
print('Test accuracy:', score[1])
score 변수의 두 번째 항목인 정확도를 출력한다. 최종 오차는 0.08, 정확도는 0.98이 나온 것을 확인할 수 있다.
predicted_classes = np.argmax(model.predict(X_test), axis=1)
correct_indices = np.nonzero(predicted_classes == y_test)[0]
incorrect_indices = np.nonzero(predicted_classes != y_test)[0]
▶ 실행 결과
x_train shape (60000, 28, 28)
y_train shape (60000,)
x_test shape (10000, 28, 28)
y_test shape (10000,)
지금까지 심층 신경망 모델의 구조를 만들고 그 모델을 학습시킨 후 학습 결과까지 살펴보았다. 이제 실제로 인공지능이 어떤 그림을 무엇으로 예측했는지 잘 구분한 그림과 잘 구분하지 못한 그림을 살펴보자.
predicted_classes = np.argmax(model.predict(X_test), axis=1)
model에서 결과를 예측하는 함수인 predict 함수에 X_test 데이터
를 입력해 보자. X_test 데이터의 개수는 1만 개였다. 따라서
예측한 값 또한 1만 개가 나오며, 그 모습은 다음 그림과 같다.

X_test의 예측값
argmax 함수를 사용한다. argmax 함수는 여러 데이터 중에서 가장 큰 값이 어디에 있는지 나타내기 때문이다.
argmax 함수를 사용하기 위해서는 열 중에서 가장 큰 것을 고를지, 행 중에서 가장 큰 것을 고를지 알려 주어야 한다. 이때 기준을 정하는 것이 바로 axis이다. axis=0은 각 열(세로)에서 가장 큰 수를 고르는 것이고, axis=1은 각 행(가로)에서 가장 큰 수를 고르는 것이다. 우리는 각 행(가로)에서 가장 큰 값을 찾아야 하기 때문에 axis=1로 설정한다.
그 결과 첫 번째 넣은 데이터 정답이 6이라는 것을 알 수 있다. 이제 argmax 함수를 사용하여 인공지능 모델이 예측한 모든 값을 predicted_classes 변수에 넣는다
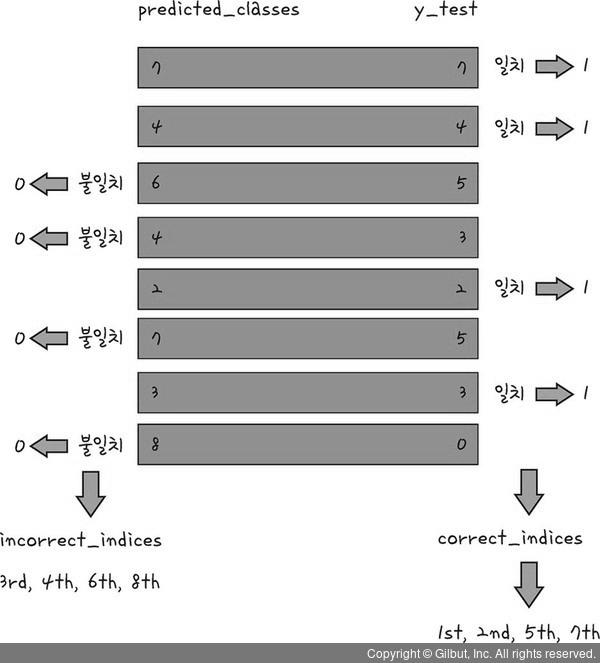
correct_indices = np.nonzero(predicted_classes == y_test)[0]
correct_indices 변수에 저장한다.
nonzero 함수
predicted_classes)과 실젯값(y_test)를 비교해 보자. 먼저 2개의 값이 일치하는(==,프로그래밍에서 같다는 의미는 ==로 표시한다) 값을 찾는다. 즉,어떤 그림을 정확하게 예측했는지 살펴보는 과정이다.
논리 연산의 결과 두 값이 같으면 1(참),같지 않으면 0(거잣)이 나온다. 앞의 코드에서는 예측한 결괏값(predicted_classes)과 실제 결팟값(y_test)의 데이터를 비교하여 결과가 같으면 1이,다
르면 0이 나온다.
같은 값을 찾기 위해서 1만 개의 수 모두를 하나하나 확인하기란 쉽지 않다. 이때 사용할
수 있는 함수가 바로 넘파이 함수의 nonzero 함수이다. nonzero 함수는 넘파이 배열에서 0이 아닌 값,즉 여기에서는 1(인공지능이 예측한 값과 정답이 일치하는 수)을 찾아내는 함수이다. 이 함수를 사용하면 다음과 같이 정확하게 예측한 데이터 위치를 알아낸다. 이제 nonzero 함수를 사용하여 0이 아닌 값(여기에서는 1 인 값)을 찾아 준다. 이때 정확하게 예측한 데이터 위치,즉 첫 번째. 두 번째, 다섯 번째, 일곱 번째 ∙∙∙를 correct_indices 변수에 넣어 준다.
incorrect_indices = np.nonzero(predicted_classes != y_test)[0]
incorrect_indices변수에 저장하되, 바로 윗줄 의 코드와 다른 점은 일치하지 않는(!=,프로그래밍에서 같지 않다는 의미는 !=로 표시한다) 값을 찾는다. 따라서 윗줄 코드와는 달리,논리 연산의 결과 예측값과 실젯값이 같으면 0(거짓), 같지 않으면 1(참)의 값이 나온다. 마찬가지로 nonzero 함수를 사용하여 일치하지 않는 값을 찾는다.
incorrect_indices 변수에 넣는다. 결과적으로 incorrect_indices 변수에는 인공지능이 정확하게 예측하지 못한 데이터 위치가 저장된다.
plt.figure()
for i, correct in enumerate(correct_indices[:9]):
plt.subplot(3,3,i+1)
plt.imshow(X_test[correct].reshape(28,28), cmap='gray', interpolation='none')
plt.title("Predicted {}, Class {}".format(predicted_classes[correct], y_test[correct]))
plt.tight_layout()
이제 정확하게 예측한 데이터 위치와 그렇지 않은 데이터 위치를 알게 되었다.
그렇다면 그 데이터는 어떻게 생겼는지 확인해 보자.
실제로 우리가 그 결과를 눈으로 살펴볼 수 있도록
matplotlib 라이브러리를 사용해서 화면에 그래프를 출력해 보자.
실행 결과를 보면 총 9개의 이미지가 나타나며,예측값과 실젯값이 보인다. 가장 첫 번째 그림을 보면 예측값은 7이고 실젯값은 7로 정확하게 예측한 것을 볼 수 있다.

nonzero 함수
출처: https://07lee.tistory.com/87
각 코드 의미를 더 자세히 보자.
plt.figure()
matplotlib을 사용하여 그래프를 그리려면 그래프를 그리겠다는 명령을 먼저 수행해야 한다.
그 명령어가 바로 figure 함수이다. 이것을 사용하여 그림을 그릴 도화지를 준비한다.
for i in range(9):
for 반복문으로 지금부터 9개의 그림을 그린다.
plt.subplot(3,3,i+1)
for문 내부이다.
그러므로 4칸(들여쓰기 권장값)을 띄우고 코드를 입력한다.
subplot 함수는 그림 위치를
정해 주는 함수로,3개의 인자(argument)가 들어간다. 첫 번째 인자는 그림의 가로 개수이고,
두 번째 인자는 그림의 세로 개수이다.
마지막 인자는 순서이다.
이와 같이 subplot(3,3,i+1)로 지정하면
가로 3개,세로 3개의 그림을 그릴 것이고,지금 그림은
i+1 번째에 넣는다.
첫 번째 반복에서는 i 값이 0이고 i+1 값이 1이기 때문에 첫 번째에 넣는
다는 의미가 된다. 반복하면서 9번째 그림까지 순서대로 넣는다.
correct = correct_indices[i]
for문 내부이다. 4칸을 띄우고 코드를 입력한다.
앞에서 만든 correct_indices 배열에서
첫 번째부터 아홉 번째까지 값을 반복할 때마다 correct 변수에 넣는다.
첫 번째 반복에서 i 값은 0이라고 가정해 보자.
그러면 correct 변수에는 정답을 모아 놓은 배열인
correct_indices의 첫 번째 값이 들어간다.
이 예제에서는 0(첫 번째 숫자 데이터) 값이 들어간다
plt.imshow(X_test[correct].reshape(28,28), cmap='gray', interpolation='none')
for문 내부이다. 4칸을 띄우고 코드를 입력한다.
imshow 함수는 어떤 이미지를 보여 줄지 그 내용을 담고 있다.
첫 번째 반복에서는 X_test 변수에 들어 있는 첫 번째 그림
(correct 변수에 첫 번째 그림을 의미하는 0이 들어 있으니까)을 가져온다.
하지만 이 그림은 각 데이터가 28×28 형태가 아니라
각 데이터가 한 줄로 늘어선 모습을 하고 있다.
우리가 처음에 데이터를 한 줄로 바꾸었기 때문이다.
이 형태를 다시 28×28 형태로 바꾸어 주어야 하는데,
이때 사용하는 함수가 바로 reshape(28,28) 함수이다.
그리고 그림을 회색조로 나타내기 위해 cmap='gray'를 입력한다.
plt.title("Predicted {}, Class {}".format(predicted_classes[correct], y_test[correct]))
for문 내부이다. 4칸을 띄우고 코드를 입력한다.
이는 그림 설명을 넣는 코드이다.
예측한 값을 나타내기 위해 Predicted {(값이 들어가는 공간)}에
예측한 결괏값(predicted_classes[correct])을 넣는다.
그리고 실젯값을 나타내고자 Class {(값이 들어가는 공간)}에
실젯값(y_test[correct])을 넣는다.
이때 format 함수를 사용하여 값을 넣어 준다.
plt.tight_layout()
tight_layout 함수를 사용한다.
실행 결과를 보면,왼쪽 위부터 첫 번째 이미지에 대한 예측 결과와 실젯값이 표시된 모습을 볼 수
있다. 첫 번째 이미지를 예측한 값(Predicted)은 7이고,
실젯값(Class) 또한 7이다.
두 번째 이미지 또한 예측한 값(Predicted)은 2고,실젯값(Class)도 2이다.
plt.figure()
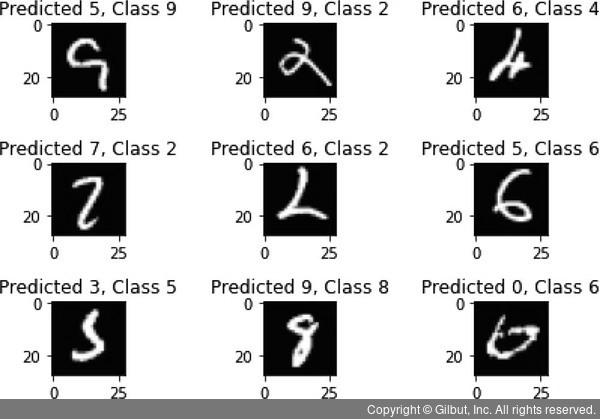
for i, incorrect in enumerate(incorrect_indices[:9]):
plt.subplot(3,3,i+1)
plt.imshow(X_test[incorrect].reshape(28,28), cmap='gray', interpolation='none')
plt.title("Predicted {}, Class {}".format(predicted_classes[incorrect], y_test[incorrect]))
plt.tight_layout()
이제 어떤 숫자를 잘 예측하지 못했는지 살펴보자.
코드는 앞의 코드,즉 잘 예측한 데이터 살펴보기 코드와 동일한다.
하지만 변수만 잘 예측하지 못한 그림으로 바뀔 뿐이다.
nonzero 함수
출처: 길벗
맞다. 생각보다 인공지능 성능이 높지 않다. 왜 그럴까?
바로 인공지능 모델 학습이 잘되지 않았기 때문이다.
인공지능 모델 학습이 잘되려면 모델의 학습 횟수를 늘려야 한다.
plt.figure()
matplotlib을 사용하여 그래프를 그리려면 그래프를 그리겠다는 명령을 먼저 수행해야 한다. 그 명령어가 바로 figure 함수이다.
이것을 사용하여 그림을 그릴 도화지를 준비한다.
for i in range(9):
for 반복문으로 지금부터 9개의 그림을 그린다.
plt.subplot(3,3,i+1)
for문 내부이다. 그림 순서를 정해 준다.
incorrect = incorrect_indices[i]
for문 내부이다.
앞에서 만든 incorrect_indices 배열에서 첫 번째부터 아홉 번째까지 값을
반복할 때마다 incorrect 변수에 넣는다.
첫 번째 반복에서 i 값은 0이다. 이때 incorrect_indices 배열의 첫 번째 값이 13이라고 가정해 보자.
이는 13번째 그림을 맞히지 못했다는 의미고,incorrect 변수에는 13이 들어간다.
plt.imshow(X_test[incorrect].reshape(28,28), cmap='gray', interpolation='none')
for문 내부이다.
imshow 함수는 어떤 이미지를 보여 줄지 그 내용을 담고 있다.
첫 번째 반복에서는 X_test 변수에 들어 있는
13번째 그림(incorrect 변수에 13이 들어 있으니까)을 가져온다.
그림 형태를 바꾸기 위해 reshape(28,28) 함수를 사용하고,
마찬가지로 그림을 회색조로 나타내기 위해 cmap='gray'를 입력한다.
plt.title("Predicted {}, Class {}".format(predicted_classes[incorrect], y_test[incorrect]))
for문 내부이다. 이는 그림 설명을 넣는 코드이다.
예측한 값을 나타내기 위해 Predicted {(값이 들어가 는 공간)}에
예측한 결괏값(predicted_classes[incorrect])을,
실젯값을 나타내기 위해 Class {(값이 들어가는 공간)}에
실젯값(y_test[incorrect])을 넣는다.
이때 format 함수를사용하여 값을 넣어 준다.
plt.tight_layout()
tight_layout 함수를 사용한다. 실행 결과를 보면 화면의 왼쪽 위부터 첫 번째 이미지에 대한 예측값과 실젯값이 표시된 모습을 볼 수 있다. 첫 번째 이미지를 예측한 값(Predicted)은 6이지만 실젯값(Class)은 5이다. 두 번
째 이미지 또한 예측한 값(Predicted)은 9이지만,실젯값(Class)은 2이다.
과적합 문제가 생길 수 있다. 인공지능 모델의 학습 횟수를 무작정 늘린다고 해서 인공지능 성능이 계속 좋아지는 것은 아니다. 바로 과적합(overfitting) 문제가 일어날 수 있기 때문이다.
과적합이란 인공지능이 훈련 데이터에만 최적화되는 것을 의미한다. 인공지능 모델을 계속 학습시킨다면 인공지능 모델이 학습하고 있는 데이터,즉 훈련 데이터만 잘 구별할 수 있다. 이 경우 새로운 데이터인 검증 데이터를 인공지능 모델에 넣었을 때 잘 구별하지 못하는,
즉 성능이 나빠지는 현상을 볼 수 있다.
이러한 현상을 바로 '과적합(overfitting)’이라고 한다. 그렇기 때문에 인공지능 모델을 학습시킬 때 얼마만큼 학습시키는 것이 좋은지 결정하는 것 또한 인공지능 모델 설계에서 중요한 부분이다.
지금까지 첫 번째 인공지능인 숫자를 구분하는 인공지능을 만들어 보았다. 갑자기 어려운 코드 들이 나와서 많이 당황스러웠을 수 있다. 코드 하나하나를 세부 의미까지 이해하는 것도 중요하지만 딥러닝의 개발 흐름을 알아보는 것이 이 책 목표이기에 전반적인 흐름을 먼저 이해하길 추천한다. 우리가 설계한 모델 이외에 수많은 새로운 모델을 다양하게 만들 수 있다. 레이어 수나 각 레이어의 노드 수, 활성화 함수, 에포크 수 등 다양한 파라미터를 수정하여 인공지능을 설계할 수 있다.
숫자를 구분하는 인공지능은 우리가 만든 방법 이외에도 CNN(합성곱 신경망)이라는 방법을 사용하여 만들 수 있다. CNN은 이미지를 인식하는 데 높은 성능을 보이고 있기 때문에 영상 인식 분야에서 주로 사용된다. 우리가 만든 이 신경망이 여러 신경망 알고리즘의 기초가 된다. 이 신경망을 기초로 하여 순환 신경망, 생성적 적대 신경망 등 다양한 딥러닝 알고리즘이 만들어지게 되었다. 그만큼 기초가 되는 신경망이라고 할 수 있다. 따라서 지금까지 잘 따라왔다면 앞으로 살펴볼 딥러닝의 심화된 모델을 학습할 준비가 된 것이다.